Алгоритмизация и Программирование
Морозов Владимир Игоревич
Формализация понятия «алгоритм»
Постановка проблемы
- На определённом этапе своего развития наука столкнулась с тем, что для решения некоторых задач алгоритмов не существует
- Чтобы доказать такое утверждение для какой-либо задачи, возникла необходимость уточнить само понятие «алгоритм»
- В рамках данной лекции будет рассмотрено несколько способов такого уточнения
Машина Тьюринга
- В 1936 году Алан Тьюринг ввёл понятие машины Тьюринга для формализации понятия алгоритма
- Она представляет собой простейшую вычислительную машину с линейной памятью
Машина Тьюринга
Машина состоит из:
- Бесконечной в обе стороны ленты, разделённой на ячейки, в каждой из которых может быть записан один символ некотрого алфавита
- Головки, которая может последовательно передвигаться по ячейкам ленты, читая и записывая символы
- Набора правил перехода, согласно которым действует головка
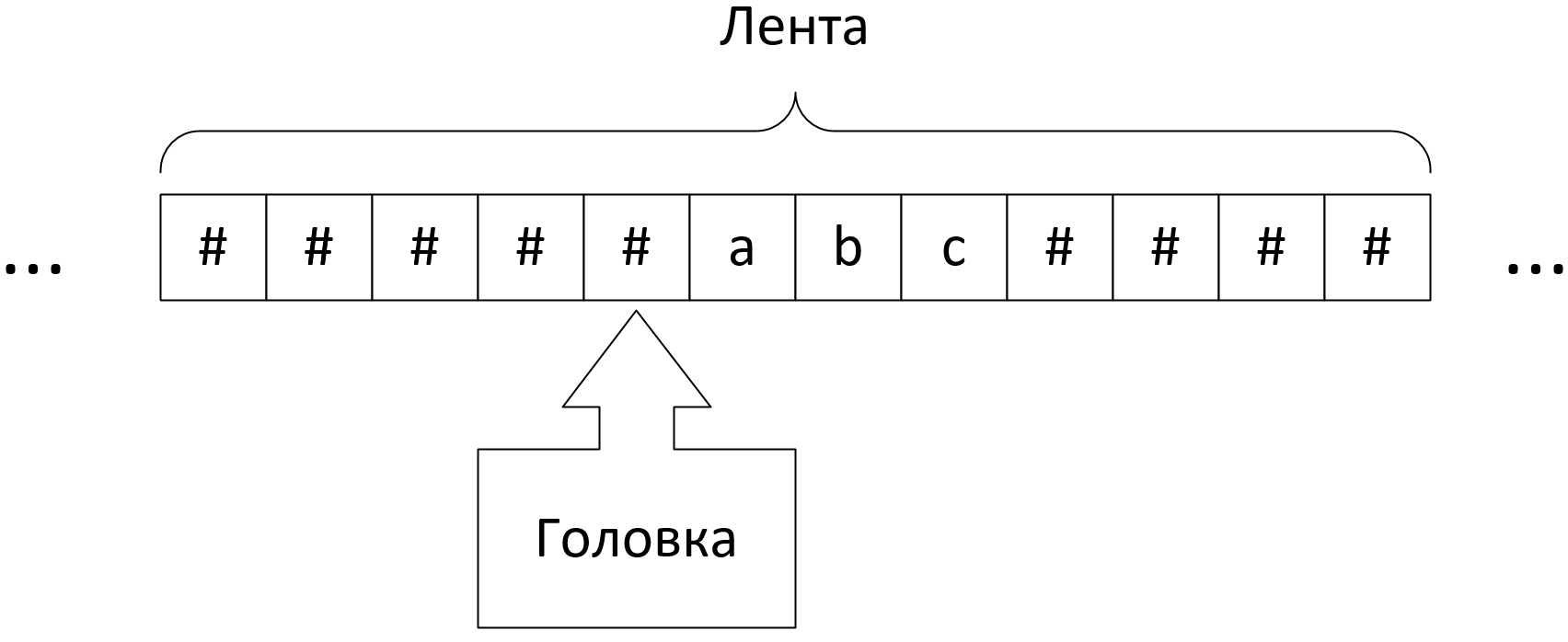
Графическое представление
Принцип работы
- Изначально на ленту помещены символы, представляющие входные данные
- Остальные ячейки при этом заполнены пустыми символами $\#$
- Головка располагается в ячейке, предшествующей первому символу входных данных
- По окончании работы на ленте остаются выходные данные и головка так же располагается перед ними
Принцип работы
- Преобразование входных данных в выходные происходит по правилам перехода, которые, по сути, представляют программу для Машины
- Правила организуются следующим образом $$q_ia_j \rightarrow q_{i'}a_{j'}d_k,$$
-
где:
- $q_i$ – текщуее состояние машины
- $a_j$ – символ, на котором стоит головка
Принцип работы
- продолжение:
- $q_{i'}$ – новое состояние машины
- $a_{j'}$ – символ, на который заменяется текущий
-
$d_k$ – направление перемещения головки:
- $L$ – шаг влево
- $R$ – шаг вправо
- $N$ – остаться на месте
Принцип работы
Таким образом, правило $q_ia_j \rightarrow q_{i'}a_{j'}d_k$ можно интерпретировать, как:
«Если машина находится в состоянии $q_i$ и головка в данный момент установлена на ячейке, содержащей символ $a_j$, нужно перейти в состояние $q_{i'}$, записать в текущую ячейку символ $a_{j'}$ и переместиться в направлении $d_k$»
Принцип работы
- Машина может иметь любое конечное число состояний
- При этом выделяются, как минимум, два состояния, которые должны быть у каждой машины: $q_0$ и $q_Z$
- $q_0$ – начальное состояние машины, в котором она находится при запуске
- $q_Z$ – конечное состояние машины, при переходе в которое её работа прекращается
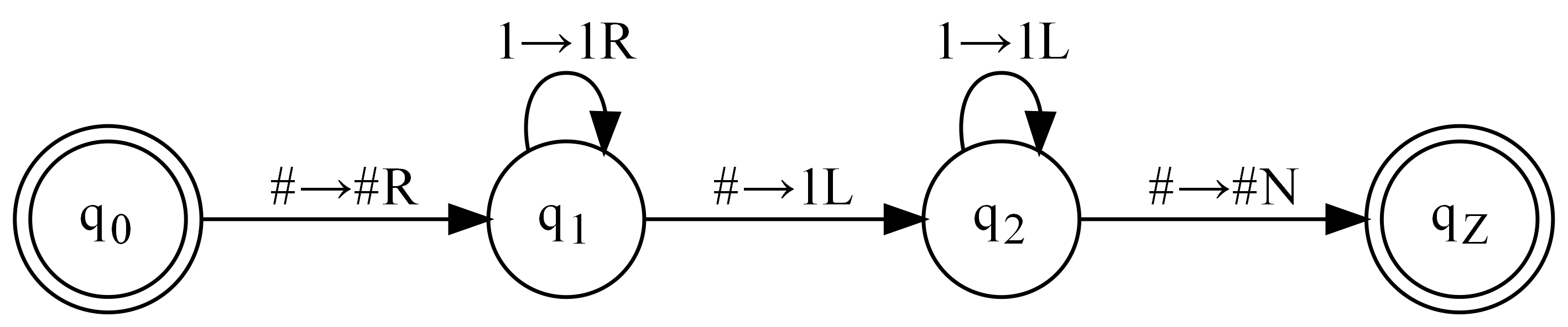
Пример $1$
- Пусть есть задача: дано число в унарной системе счисления, необходимо увеличить значение этого числа на 1
- Представим правило перехода для машины Тьюринга, решающей эту задачу: $$q_0\# \rightarrow q_Z1L$$
- Правило гласит, что нужно записать $1$ в начальную позицию, сдвинуться на ячейку влево и завершить работу
Пример $2$
- Представим набор правил перехода для решения аналогичной задачи, но с увеличением на $2$: $$ q_0\# \rightarrow q_11L\\ q_1\# \rightarrow q_Z1L\\ $$
Пример $3$
- Представим набор правил перехода для решения аналогичной задачи, но с записью новой единицы справа: $$ q_0\# \rightarrow q_1\#R\\ q_11 \rightarrow q_11R\\ q_1\# \rightarrow q_21L\\ q_21 \rightarrow q_21L\\ q_2\# \rightarrow q_Z\#N $$
Табличная запись
- Можно представить эти правила в виде таблицы
| $\#$ | $1$ | |
|---|---|---|
| $q_0$ | $q_1\#R$ | $-$ |
| $q_1$ | $q_21L$ | $q_11R$ |
| $q_2$ | $q_Z\#N$ | $q_21L$ |
Табличная запись
- Прочерк в таблице означает, что данная комбинация символа и состояния никогда не достигается
- Из того факта, что правила переходов удобно представлять в виде таблицы, можно понять, что количество правил переходов ограничено сверху количеством состояний, умноженным на количество символов ленточного алфавита
Граф переходов
Формальное определение
Машину Тьюринга $T$ можно определить как следующий кортеж: $$T = (\Gamma, \Sigma, Q, Q_0, Q_Z, \delta),$$ где:
- $\Gamma$ – ленточный алфавит
- $\Sigma$ – входной алфавит ($\Sigma \subseteq \Gamma$)
- $Q$ – множество состояний машины
Формальное определение
- $Q_0$ и $Q_Z$ – множества начальных и конечных состояний машины соответственно
- $\delta$ – множество правил переходов, при этом: $$\delta: (Q \setminus Q_Z) \times \Gamma \rightarrow Q \times \Gamma \times \{L, N, R\}$$
- Стоит также отметить, что все множества, входящие в состав МТ, конечны
Свойства
Основное свойство машины Тьюринга выражено Тезисом Тьюринга:
Если для вычисления некоторой функции существует алгоритм, значения этой функции могут быть вычислены с помощью машины ТьюрингаСвойства
- Таким образом, Тезис Тьюринга гласит, что любой алгоритм может быть запрограммирован на машине Тьюринга, это называется полнота по Тьюрингу
- В частности, алгоритм работы самой машины Тьюринга также может быть запрограммирован на машине Тьюринга, т.е. машина может моделировать сама себя
Применения
- Чтобы доказать, что некоторая система (например, язык программирования) может выполнить любой существующий алгоритм, достаточно показать, что с помощью этой системы можно моделировать работу машины Тьюринга
- Такая система называется Тьюринг-полной
- Чтобы доказать, что не существует алгоритма, решающего какую-либо проблему, достаточно показать, что решение проблемы нельзя получить на машине Тьюринга
Примеры Тьюринг-полных систем
- Все современные ЯП (SQL не входит в это понятие)
- Машина Поста
- Нормальные алгоритмы Маркова
- Игра «Жизнь»
Машина Поста
- В 1936 году (после Тьюринга) Эмиль Пост предложил свой вариант абстрактной вычислительной машины
- Машина Поста во многом похожа на машину Тьюринга, но имеет более простую систему команд
- В её состав так же входят бесконечная лента, разделённая на ячейки и головка, последовательно перемещающаяся по ней
Отличия
- Алфавит состоит всего из двух символов: $1$ и $0$, при этом $0$ также играет роль пустого символа
- Все команды в программе делятся на $6$ типов и пронумерованы
Типы команд
- $Vj$ – установить $1$ и перейти к $j$-ой строке программы
- $Xj$ – установить $0$ и перейти к $j$-ой строке программы
- $\leftarrow j$ – сдвинуться влево и перейти к $j$-ой строке программы
- $\rightarrow j$ – сдвинуться вправо и перейти к $j$-ой строке программы
Типы команд
- $?j_1:j_2$ – если в ячейке $0$ перейти к строке $j_1$ иначе перейти к строке $j_2$
- $!$ – остановить выполнение
Пример
В качестве примера напишем программу для дозаписи $1$ справа
- $\rightarrow 2$
- $?3:1$
- $V4$
- $\leftarrow 5$
- $?6:4$
- $!$
Вывод
- Несмотря на простоту, машина Поста является полной по Тьюрингу, что в очередной раз показывает, насколько простого инструментария достаточно, чтобы иметь возможность выполнить любой существующий алгоритм
Нормальные алгоритмы Маркова
- В конце 1940-ых годов А.А. Марков ввёл понятие нормального алгоритма
- Нормальные алгоритмы так же, как и машины Тьюринга и Поста, могут использоваться для формализации понятия алгоритма в целом
- Нормальные алгоритмы Маркова (НАМ) являются полной по Тьюрингу системой, хотя не включают в своё описание никаких механических устройств наподобие ленты или головки
Способ задания
- НАМ предназначены для обработки символьных строк в каком-либо алфавите
- Конкретный алгоритм определяется алфавитом и схемой – упорядоченным набором формул подстановки
- Формула подстановки – запись вида $L \rightarrow D$ или $L \rightarrow \cdot D$, где $L$ и $D$ – произвольные слова алфавита
Принцип работы
- Изначально на вход алгоиртму подаётся некоторая строка
- На каждом шаге выполнения из всех формул подстановки выбирается первая (по порядку), левая часть которой совпадет с какой-то частью текущей строки
- Если такая формула найдена, то часть текущей строки, совпадающая с левой часть формулы, заменяется на правую часть формулы
Принцип работы
- Если же подходящая формула не найдена, алгоритм завершает работу
- После замены алгоритм переходит к следующему шагу, если в выбранной формуле использовано $\rightarrow$ и останавливается, если использовано $\rightarrow \cdot$
Пример $1$
Алгоритм дописывания $1$ справа в НАМ задаётся тривиально (здесь $\Lambda$ – пустая строка)
- $1 \Lambda \rightarrow \cdot 11$
- $\Lambda \rightarrow \cdot 1$
Пример $2$
- $|b\ \ \to\ ba|$
- $ab\ \to\ ba$
- $b\ \ \ \to \Lambda$
- $*|\ \ \to\ b*$
- $*\ \ \ \to\ c$
- $|c\ \ \to\ c$
- $ac\ \to\ c|$
- $c\ \ \ \to\cdot \Lambda$
$|*||$
$|b*|$
$ba|*|$
$a|*|$
$a|b*$
$aba|*$
$baa|*$
$aa|*$
$aa|c$
$aac$
$ac|$
$c||$
$||$
Полезные источники
- EN Robin Gandy. The universal Turing Machine: A Half-Century Survey. Глава 2 – Очень подробно и понятно про роль машин Тьюринга в алгоритмизации
- RU Подробная статья про все три системы
- RU Лекция про машину Тьюринга от преподавателя из МФТИ
- RU Цикл лекций по АиТВ от профессора Кузнецова из ВШЭ (по машине Тьюринга первые две)