Постановка проблемы

• На данный момент были рассмотрены смежные и связные структур данных
• Часть из них позволяет быстрый поиск элементов (например, двоичный поиск в массиве)
• Другие – быструю вставку (например, двусвязные списки)
• Можно попробовать объединить эти преимущества

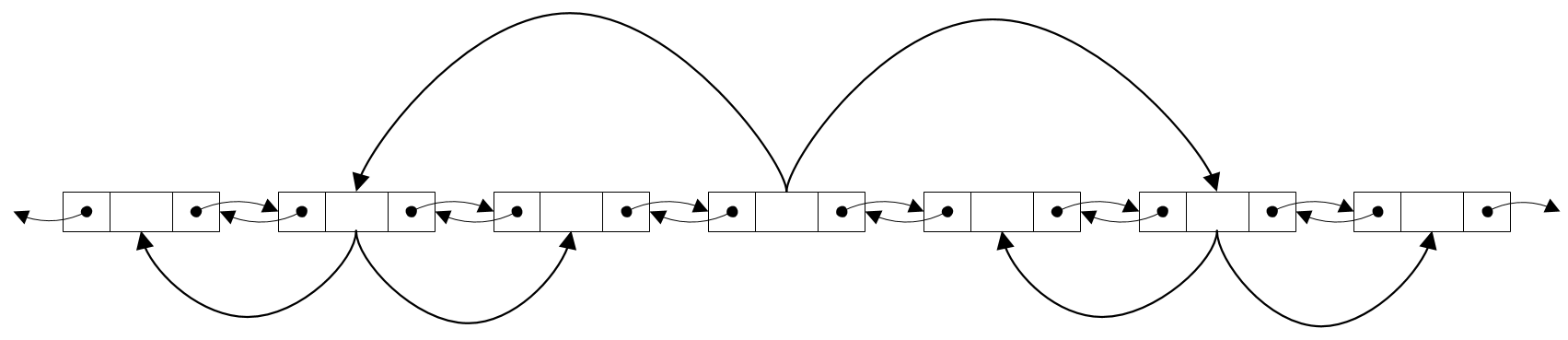
Двоичный поиск в списке

Чтобы получить быстрый двоичный поиск в связном списке, нужно, чтобы каждый его элемент хранил, помимо указателей на своих соседей, указатель на середины правой и левой половин списка

Двоичное дерево

• Структурой данных, в наиболее удобном виде представляющей то, что было представлено на предыдущем слайде, является двоичное дерево
• Это связная структура данных, каждый элемент которой имеет три указателя: на узел-«родитель» и на своего правого и левого «потомка»

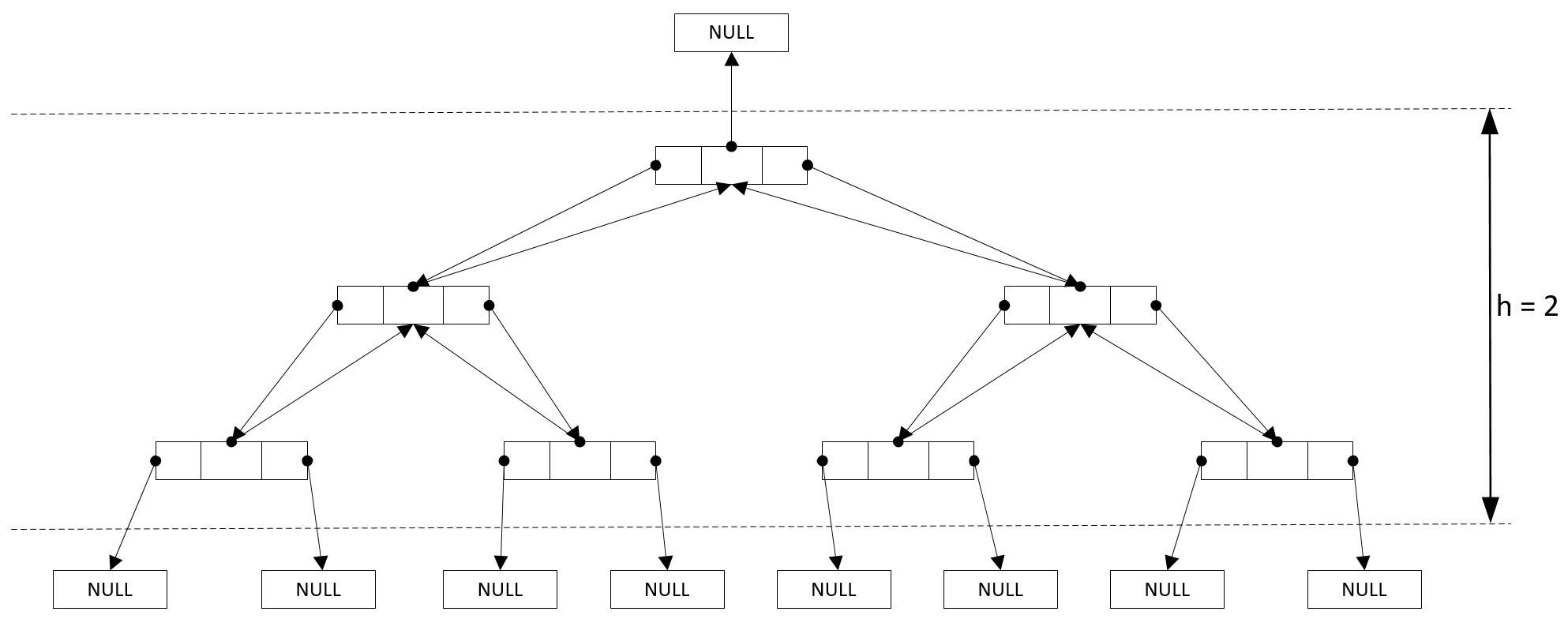
Двоичное дерево

Параметры двоичного дерева

• В рамках данной лекции наиболее интересными для рассмотрения являются два параметра двоичного дерева:
  1. Количество узлов в дереве $N$
  2. Высота дерева $h$ – количество ветвей от корня до листа
• Данные параметры связаны соотношением $$h = \lfloor log_2(N) \rfloor $$

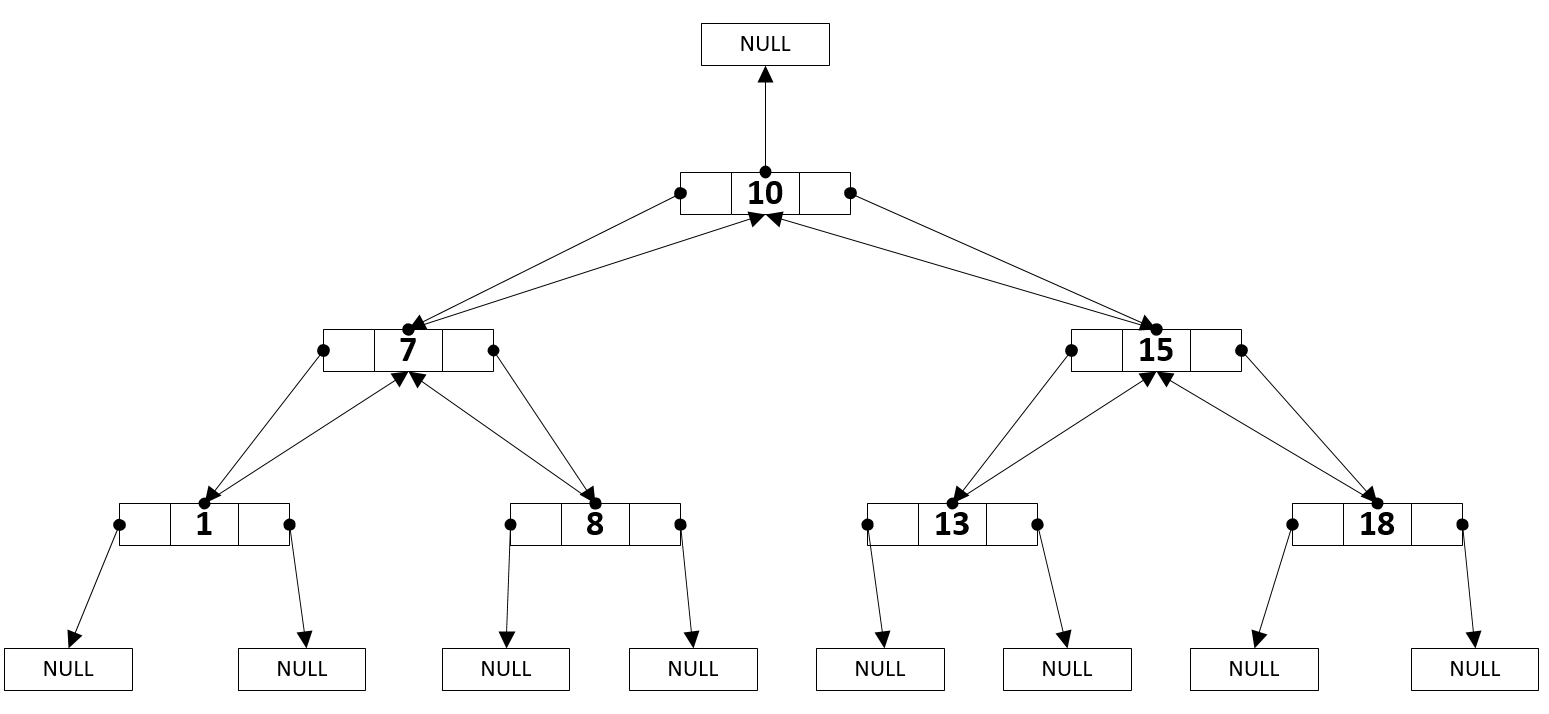
Двоичное дерево поиска

• Чтобы в представленной структуре можно было эффективно осуществлять поиск, оно должно удовлетворять правилу двоичного дерева поиска (BST):

Для каждого узла все элементы в его левом поддереве меньше него, а элементы в правом поддереве больше или равны ему

Двоичное дерево поиска

Операции над BST

Для двоичного дерева поиска могут быть эффективно реализованы следующие операции:

• Обход элементов по возрастанию (или убыванию)
• Поиск элемента по ключу
• Поиск максимального и минимального элементов
• Поиск следующего и предыдущего элемента (по возрастанию)
• Вставка элемента в дерево
• Удаление элемента из дерева

Обход элементов

• Чтобы обойти все элементы двоичного дерева поиска по возрастанию, необходимо для каждого из узлов обойти его левое поддерево, потом его собственный элемент и, наконец, правое поддерево
• Под обходом поддерева понимается выполнение той же процедуры рекурсивно для поддерева
• Сложность обхода дерева – $\Theta(N)$, т.к. для каждого узла процедура вызывается дважды: для его левого и правого поддерева

Обход элементов

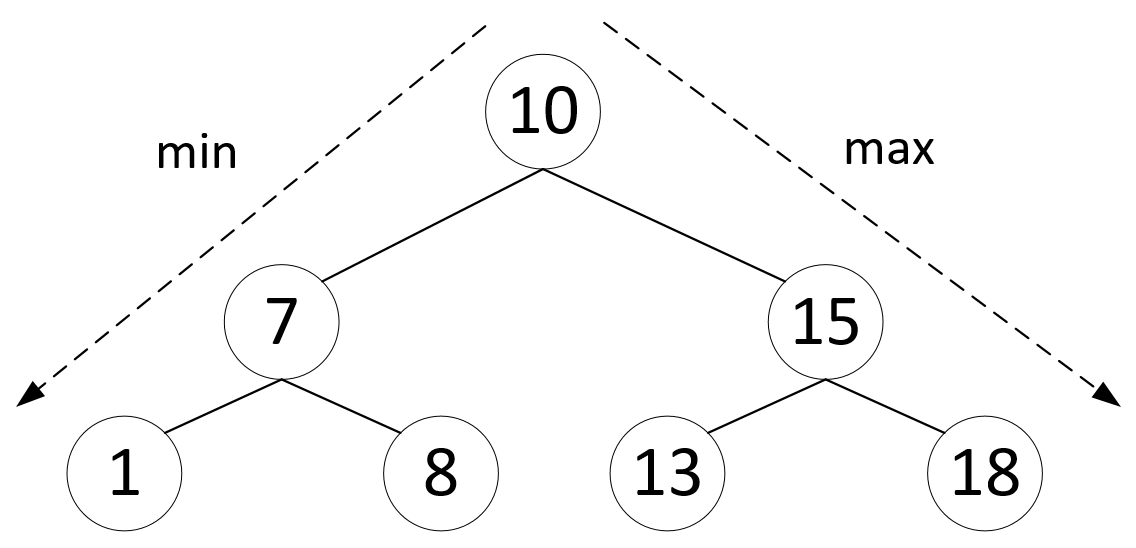
Поиск min и max элементов

• Благодаря свойству двоичного дерева поиска, минимальный и максимальный элементы всегда располагаются в самом левом и самом правом листе дерева соответственно
• Сложность поиска максимального и минимального элементов – $O(h)$, т.к. посещённые при поиске узлы образуют простой нисходящий путь, т.е. каждый уровень дерева посещается один раз

Поиск min и max элементов

Поиск элемента по ключу

Чтобы найти элемент с заданным ключом, в дереве выполняется следующий алгоритм:

1. Если значение в текущем узле равно искомому, вернуть текущий узел
2. Если искомое значение больше или равно текущему, продолжить поиск в правом поддереве
3. Если искомое значение меньше текущего, продолжить поиск в левом поддереве
4. Если встречено значение $NULL$, элемент не найден

Поиск элемента по ключу

Сложность поиска максимального и минимального элементов – $O(h)$, т.к. посещённые при поиске узлы образуют простой нисходящий путь

Поиск элемента по ключу

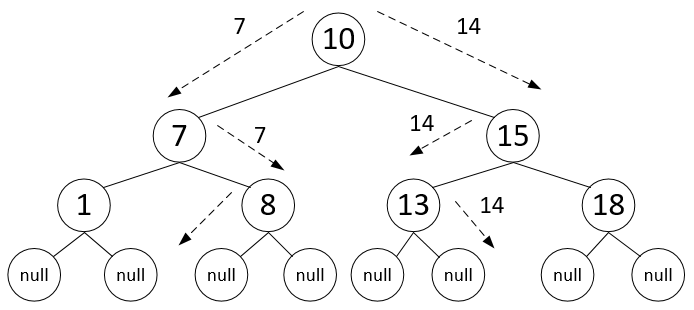
Пунктирными стрелками на рисунке представлены пути обхода дерева для поиска элементов 8 (удачного) и 14 (неудачного).

Вставка элемента в дерево

• Для вставки элемента в дерево необходимо выполнить поиск элемента
• В случае, если элемент нашёлся, следует продолжать поиск в правом поддереве
• Когда встретится $NULL$, на его место нужно поставить вставляемый элемент
• Аналогично рассмотренным ранее алгоритмам, сложность вставки элемента составляет $O(h)$, т.к. посещённые узлы образуют простой нисходящий путь

Вставка элемента в дерево

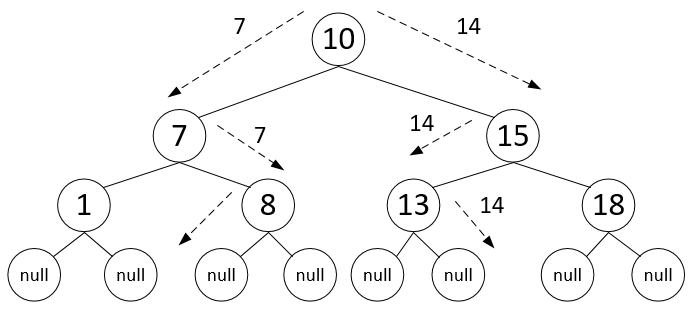
На данном слайде представлен поиск места для вставки элемента в дерево для существующего (7) и несуществующего (14) элементов

Вставка элемента в дерево

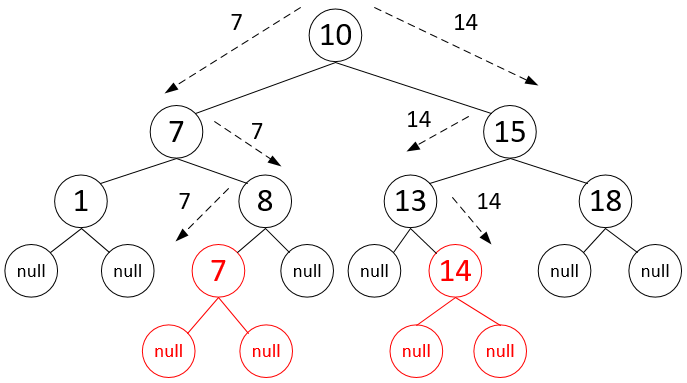
На данном слайде представлено состояние дерева после вставки элементов 7 и 14

Удаление элемента из дерева

• Удаление элемента из дерева является самым сложным алгоритмом, т.к. необходимо в любом случае сохранить свойство бинарного дерева поиска
• Т.е. найти, какой узел нужно подставить на место удалённого и как отредактировать связи

Удаление элемента из дерева

• При удалении могут возникнуть три ситуации:
  1. Удаляемый узел является листом (не имеет потомков)
  2. Удаляемый узел имеет только одного потомка
  3. Удаляемый узел имеет двух потомков

Удаление листа

В случае, если удаляемый узел является листом (не имеет потомков), он просто исключается из дерева, а на его место ставится $NULL$

Удаление с одним потомком

Удаляемый узел $z$ имеет только левого потомка (для правого аналогично)

Удаление с двумя потомками

Когда удаляемый узел имеет двух потомков, возможны две подситуации:

1. Левый потомок его правого потомка равен $NULL$
2. Левый потомок его правого потомка не равен $NULL$

Ситуация 1

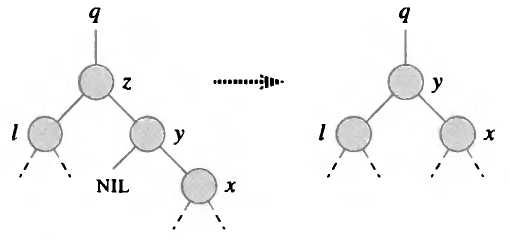
Ситуация 2

Обобщение

Обе ситуации можно обобщить одним правилом:

• В случае удаления из дерева элемента, имеющего двух потомков, этот элемент заменяется наименьшим элементом его правого поддерева
• При этом правый потомок этого наименьшего элемента становится левым потомком его родителя

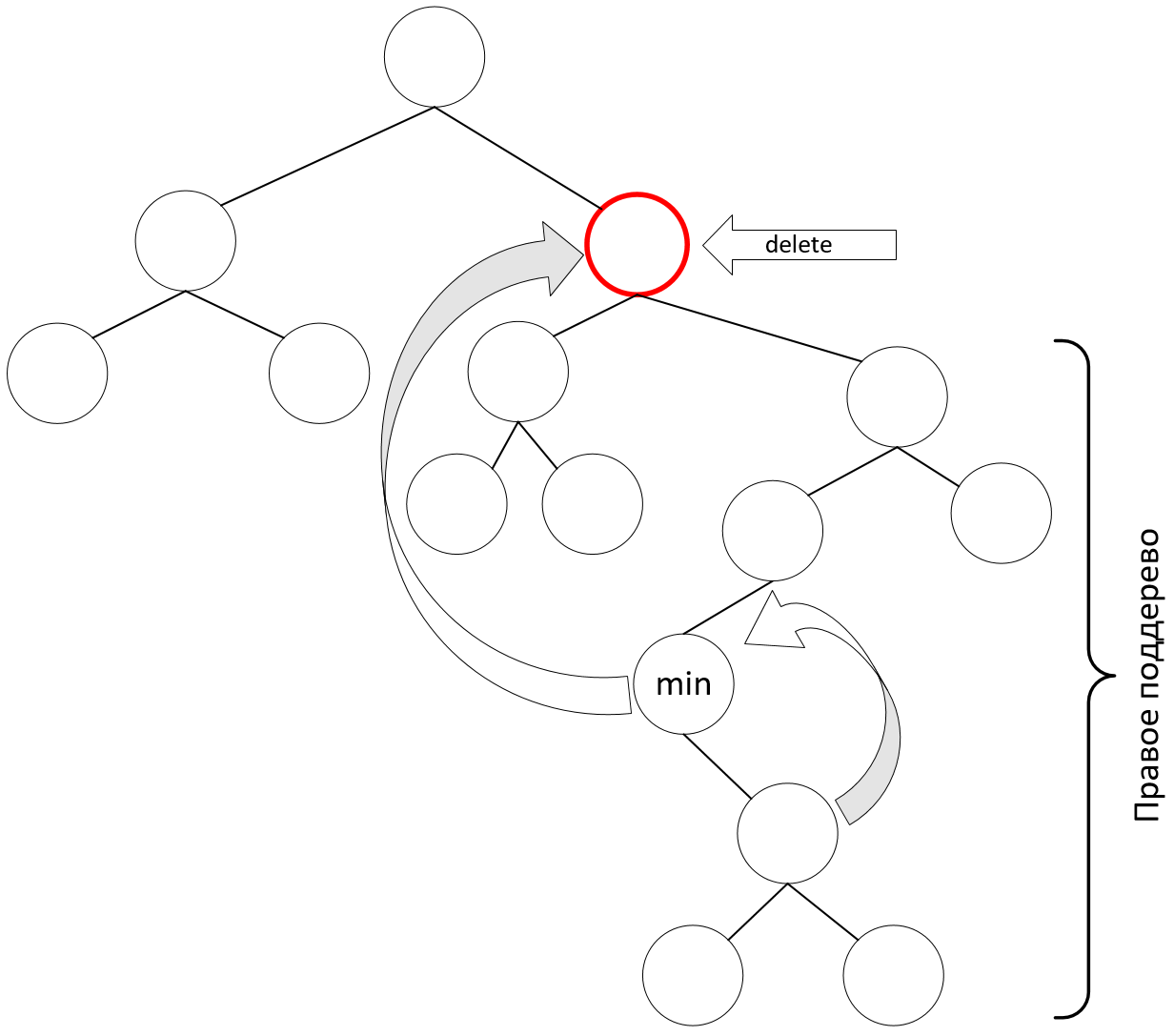
Сложность удаления

Вычислительная сложность удаления элемента из дерева в любом из случаев составляет $$O(h)$$

Поиск предыдущего и следующего элемента

Поиск следующего по возрастанию элемента учитывает два случая:

1. Если у переданного узла есть правое поддерево, в качестве следующего элемента возвращается наименьший элемент этого поддерева
2. Если правого поддерева нет, в качестве следующего элемента возвращается наименьший узел, левый потомок которого является родителем переданного

Поиск предыдущего и следующего элемента

• Поиск предыдущего элемента симметричен поиску следующего
• Оба случая имеют сложность $O(h)$

Пример

1. $next(8) = 10$, т.к. левый потомок $10$ – $7$ – является родителем для $8$
2. $next(10) = 13$, т.к. $13$ – наименьший элемент правого поддерева $10$

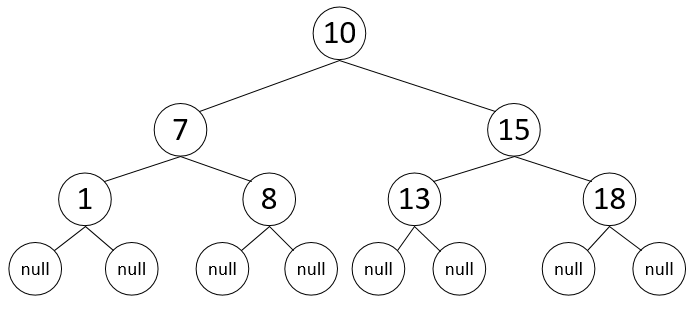
Недостаток двоичных деревьев поиска

• Двоичное дерево поиска представляет собой эффективную структуру данных, т.к. позволяет выполнять все операции за $$O(h) = O(log_2(N))$$
• Но последнее равенство справедливо только для дерева, элементы в котором распределены по ветвям равномерно

Недостаток двоичных деревьев поиска

• Представим себе дерево (след. слайд), в которое последовательно добавляется $9$ узлов, содержащих значения по возрастанию от $1$ до $9$
• В таком случае, очевидно, $h = N - 1$ и сложность всех операций снижается до $O(N)$

Недостаток двоичных деревьев поиска

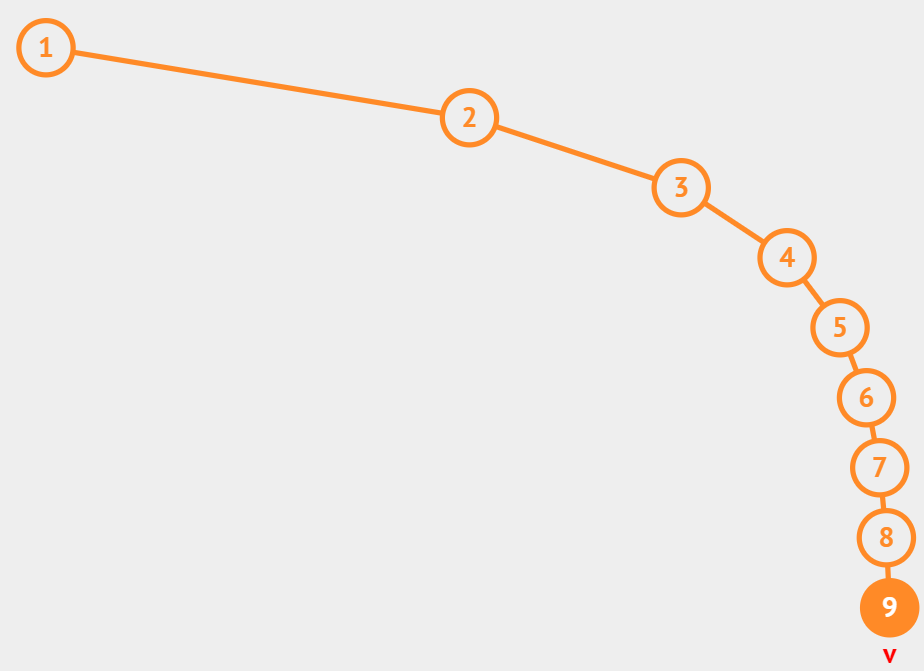
Недостаток двоичных деревьев поиска

• Несмотря на то, что доказано [2], что в случае, когда все помещаемые в дерево величины равновероятны, дерево с наибольшей вероятностью будет заполняться равномерно, показанная ситуация тоже возможна
• Эта проблема решается с помощью сбалансированных деревьев, которые будут рассмотрены на следующих лекциях

Полезные источники

1. RU С. Скиена. Алгоиртмы. Руководство по разработке. 2-е издание. Подраздел 3.4 – Более простое и краткое объяснение.
2. RU Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн. Алгоритмы: построение и анализ, 3-е издание. Глава 12 – Основная книга нашего курса.
3. RU Статья про BST

Полезные источники

4. EN Визуализация BST
5. EN Более красивая визуализация BST
6. RU Пример реализации BST на Python с подробным описанием